Resistência dos Materiais e Concreto Armado: Condições de equilíbrio de estruturas e Vínculos na engenharia estrutural

Eu li o livro “Concreto Armado Eu te amo” pela primeira vez quando eu pagava a cadeira de resistência dos materiais II, no curso técnico de edificações. Adorei a leitura os autores são bastante claros, objetivos e didáticos quanto a matéria de resistência dos materiais e concreto armado.

Hoje, após concluir meu curso volto a ler o livro novamente e pensei em compartilhar aqui uma espécie de “resumo” ou feedback dele. A intenção aqui é poder contribuir de alguma forma com a matéria e seria muito bom se houvesse uma troca de conhecimento, então deixe seu comentário seja para sugestão, correção ou qualquer outra coisa. 

CONDIÇÕES DE EQUILÍBRIO DE ESTRUTURAS

Já vimos nas postagens anteriores que ação e reação é aplicável a todas as estruturas que ao receber cargas fiquem em equilíbrio (não se move). Isso vale para as forças sejam elas horizontais, verticais, horizontais e inclinadas.  Ou seja, como resposta à ação de esforços externos as estruturas reagem, com isso as forças se anulam e ficam em equilíbrio.

Para que a estrutura seja estável, é importante entender três pontos:

1º A soma das cargas horizontais ativas e as horizontais reativas se igualem (se anulem);

2º A soma das cargas verticais ativas e reativas se igualam (se anulem);

3º A somatória dos cálculos dos momentos fletores (de rotação) para qualquer ponto de estrutura seja nulo.

Vamos fazer alguns exemplos para reforçar.

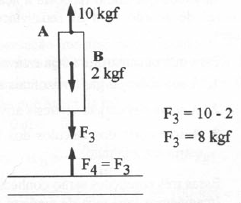
 1º Sobre essa barra vertical que soldada a uma peça é puxada com uma forçada de 10kgf no ponto A e no ponto B é empurrada com força de 2kgf.

 Olhando a estrutura e analisando as forças é notório entender que se a barra não estivesse soldada ela se movimentaria para cima com 8kgf, pois tem 10kgf puxando para cima e apenas 2kgf para baixo. E facilmente sairia do equilíbrio, pois as cargas horizontais não se anulariam (conforme o ponto 2º citado)

Porém a barra está soldada a uma peça, então para a barra não se desligar da estrutura, está terá que puxar a barra com força de 8kgf, anulando assim as forças e mantendo a barra em equilíbrio.

E se a estrutura puxa (ação) a barra com 8kgf, a barra puxa (reação) a estrutura com 8kgf. E assim todas as forças se anulam.

2º Imaginemos uma viga de madeira apoiada em dois pontos (paredes de alvenaria) e que essa viga suporta um esforço não centrado de 500gkf como é mostrado na figura a seguir. Ela é uma viga isostática, ou seja, está em equilíbrio. Vamos analisar como essa viga se comporta, no seu aspecto de equilíbrio. 

Resolução:

VÍNCULOS NA ENGENHARIA ESTRUTURAL

Chama-se vínculo de uma estrutura, cada restrição dessa estrutura ao seu giro, a um movimento vertical, ou a um movimento horizontal.

Imaginemos essa primeira estrutura

Essa barra permanecerá estável (sem movimento) quando receber esforços verticais para baixo, pois seus apoios a sustentará, e quando receber esforços horizontais para esquerda, pois a parede a qual ela está encostada impedirá que a barra se movimente. Porém esta barra será instável (se movimentará) quando receber esforços verticais para cima, horizontais para a direita e momentos anti-horários.

Já essa segunda estrutura

Graças a seus vínculos, é estável para qualquer esforço seja ele horizontal ou vertical.

Quando se estuda vigas, é comum encontrarmos a seguinte descrição de vínculos para os apoios:

Apoio carrinho, rolete ou apoio simples, o vínculo permite reagir só com forças verticais.

No apoio articulação é transmitido a estrutura reações verticais e horizontais.

Já no apoio engastamento transmite esforços verticais, horizontais e momentos.

Resistência dos Materiais e Concreto Armado: Peso Linear, Ação e Reação e Momento Fletor

Eu li o livro “Concreto Armado Eu te amo” pela primeira vez quando eu pagava a cadeira de resistência dos materiais II, no curso técnico de edificações. Adorei a leitura os autores são bastante claros, objetivos e didáticos quanto a matéria de resistência dos materiais e concreto armado.

Hoje, após concluir meu curso volto a ler o livro novamente e pensei em compartilhar aqui uma espécie de “resumo” ou feedback dele. A intenção aqui é poder contribuir de alguma forma com a matéria e seria muito bom se houvesse uma troca de conhecimento, então deixe seu comentário seja para sugestão, correção ou qualquer outra coisa. 

PESO LINEAR

Na portagem anterior vimos a relação do peso com o volume, peso específico, e a relação do peso com a área. Nesta postagem veremos a relação do peso com o comprimento, ou seja, o peso linear.

Para peças que têm seção constante (barras de aço, por exemplo), podem ter seu peso expresso por metro, válido isso para cada diâmetro.

A formula do peso linear é a relação do peso com o comprimento.

P_l = P / C ou C = P/P_l ou P = P_l x C

Vejamos um exemplo:

1º Quanto pesam 9m de uma barra de 8mm (5/16”)? Sabendo que o peso linear da barra de 8mm é 0,383kgf/m.

AÇÃO E REAÇÃO 

Para entender o efeito da ação e reação é preciso pensar a partir do seguinte postulado:

“ À cada ação (força) corresponde uma reação (força) de um mesmo valor, igual direção, mas de sentido inverso. ”

Ou seja a medida que eu aplico uma força em um corpo, haverá uma outra força (reação) que irá reagir a primeira a esta força que está sendo aplicada, as mesmas terão mesmo valor, direção porém sentidos inversos. Isso funciona para qualquer estrutura que esteja em equilíbrio visto que as forças de ação e reação irão se anular.

 

Vamos imaginar esse seguinte exemplo:

A ilustração acima é uma ponte simplificada que vence o vão de um rio suportando uma canalização de água.

Admitimos que o conjunto viga, tubo e água que passam dentro dele pesam 2450kgf/m. O peso total disso é P = 2450 X 10m = 24500kgf ou 24,5tf.

Logo, o peso desse conjunto é 24,5ftf dirigido para baixo, deve ser suportado pelos dois pilares que receberão cargas iguais (pois está sendo uniformemente distribuída não havendo razão para se pensar que ocorram cargas diferentes nos pilares P1 e P2).

Trazendo agora o que vimos na teoria sobre ação e reação para o exemplo, teremos que:

Ao ser aplicada a força (peso) de 24,5ft nos dois pilares, onde cada um receberá 12,25tf de carga, os pilares responderão (reação) com outra força do mesmo valor, da mesma direção, mas de sentido inverso.  Como na imagem.

Após a carga ser distribuída da viga para os pilares ela é transferida para a fundação que está transferirá para o terreno.

Para que os pilares fiquem estáveis, é necessário que o terreno aja sobre eles com força T1 e T2 (ascendentes) T1 não será igual a P1, pois deve receber também o peso próprio do pilar (L1), igualmente T2 será igual a P2 + L2. 

MOMENTO FLETOR

Se formos nos livros ou no google e jogar lá: momento fletor, encontraremos a seguinte definição:

“Em física, o momento, é uma grandeza que representa a magnitude da força aplicada a um sistema rotacional a uma determinada distância de um eixo de rotação. ”

Pronto, está definido momento fletor, é muito simples!

Para simplificar ainda mais, vamos imaginar aqui:

Olhando essa imagem acima temos o seguinte: uma barra vertical de comprimento h, e uma força F sendo aplicada sobre ela na distância h do seu eixo de rotação (que no caso é o encaixe ou engastamento).

Sendo assim o momento será o valor que representa a força ao sistema rotacional que está sendo aplicada na determinada distância do eixo de rotação, ou seja,

M = F x L

Se consideramos:

F = 120kgf

h = 3,5

O momento será igual a:

M = F x L   -> M = 120 x 3,5 -> M = 420kgfm.

Simples! Mas vamos pensar um pouco mais.

Como o momento é resultado do produto Força e Distância, para duas barras onde estão sendo aplicadas forças de valores iguais, porém distancias diferentes, os momentos serão diferentes.

Quanto maior a distância nesse caso maior será o momento.

A tendência a girar pode ser associada a um sentido de rotação. Assim, forças que tendem a girar a barra no sentido horário, vão gerar momentos que por mera convenção serão positivos (+) e as que tendem girar no sentido anti-horário vão gerar momentos negativos (-).

Para finalizar vamos acompanhar esse exemplo abaixo:  

Resistencia dos Materiais e Concreto Armado: Peso específico, peso por área e definição de concreto armado.

Eu li o livro “Concreto Armado Eu te amo” pela primeira vez quando eu pagava a cadeira de resistência dos materiais II, no curso técnico de edificações. Adorei a leitura os autores são bastante claros, objetivos e didáticos quanto a matéria de resistência dos materiais e concreto armado.

Hoje, após concluir meu curso volto a ler o livro novamente e pensei em compartilhar aqui uma espécie de “resumo” ou feedback dele. A intenção aqui é poder contribuir de alguma forma com a matéria e seria muito bom se houvesse uma troca de conhecimento, então deixe seu comentário seja para sugestão, correção ou qualquer outra coisa. 

PESO ESPECÍFICO

Densidade ou Peso específico de um corpo, é o índice que mede o maior peso por unidade de volume. Logo, o peso específico (Y) será a relação do peso (P) e o volume (V) do corpo.

Y = P/V ou P = Y x V ou V = P / Y

Por essa razão que se colocarmos concreto em um copo e areia em outro copo, com o mesmo volume do primeiro, teremos pesos diferentes pois a densidade dos objetos (concreto e areia) não são semelhantes.

Vejamos alguns exercícios:

1º Uma peça de madeira Cabreúva possui densidade correspondente a 980kgf, qual o peso da peça sabendo que a mesma possuí 2,7m³?

2º Qual o volume de uma peça de cedro que pesou 1,7tf? Obs.: o peso específico do cedro é 540kgf.

3º Qual o peso específico de uma madeira que apresentou em uma peça um peso de 2100kgf para um volume de 2000L?         

4º Qual o peso de uma laje de concreto armado que tem 30cm de altura, por 5m de largura e 4,20m de comprimento? Sabendo que o peso específico do concreto é 2500kgf/m³.

PESO POR ÁREA

Em carregamentos que possuem uma altura relativamente constante podemos usar o conceito de peso por área, ou seja, o peso por área é a relação do peso SOB a área

PA = P/A ou P = PA x A ou A = P / PA

Vejamos um exemplo:

1º Qual o peso que se transmite a uma laje se esta for coberta por uma área de 5,2m x 6,3m de ladrilho? O peso por área desse material é de 70kgf/m².

CONCRETO ARMADO

No decorrer do nosso estudo trabalharemos muito com concreto armado, então vamos entender um pouco sobre esse elemento construtivo presente na maioria dos elementos estruturais (lajes, fundação, pilares, vigas...).

Antes do concreto armado, os antigos utilizavam a pedra como material de construção nas suas moradias, templos, pontes entre outras coisas. Mas existia um problema com a pedra! Apesar de ser um material rígido, durável e resistente a compressão (comprimir/tentar aproximar as partículas), a pedra falhava na resistência a tração (distender/afastar as partículas). E o que isso significa?

Vejamos bem, utilizando as características da viga como exemplo:

A viga deve vencer esforços de compressão e tração, logo, quanto maior a viga maior será os esforços de tração e compressão a se vencer. No caso das pedras quando usadas como vigas para vencer vãos de médio e grande porte (pontes, por exemplo) a pedra se rompia, justamente por que não conseguia vencer os altos esforços de compressão.

Com o passar dos tempos, os romanos começaram a construir suas pontes no formato de arco, sendo assim cada peça estudada trabalhava em compressão. Porém, eram obrigados a construir múltiplos vãos.

Quando o homem passou a usar o concreto a limitação era a mesma. Mas, afinal o que é concreto? O concreto é uma “pedra” artificial fabricada através da junção de água, agregado graúdo (pedra), agregado miúdo (areia) e cimento, em média o material resiste à compressão 10 vezes mais que à tração.

Para resolver esse dilema do esforço de tração, pensou-se: “Por que não usar uma mistura de material bom para compressão e um bom para tração” Daí entra a ideia do concreto armado. A armação, ou seja, o aço (o material ótimo para resistir a tração) é mergulhado no concreto para assim resistir aos esforços de tração que o concreto sozinho não conseguiria.

No miúdo, a ideia do concreto armado é esta: misturar o concreto com uma armação para que esta venha a vencer os esforços de tração que o concreto por si só não é suficiente para vencer. Se utiliza concreto armado em quase tudo nas vigas, pilares, lajes, sapatas, estacas de fundação, já apenas o concreto é utilizado por exemplo nos blocos de fundação, tubulação de água, entre outras coisas. 

Medição de consumo de energia elétrica por mês de uma residência

Quem já viu elétrica no ensino médio ou no curso técnico sabe que medir o consumo de energia elétrica de um aparelho é algo básico e essencial.

Hoje pretendo mostrar para vocês, como calcular o consumo mensal de energia elétrica dos aparelhos comuns da sua residência, mas que pode ser aplicado a qualquer outro, ao final, você pode calcular o valor a ser pago pelo o consumo, que é a tarifa cobrada na sua conta de energia. 

Vamos seguir os passos:

1.    Ver a potência do aparelho:

Cada aparelho possui uma potência, que permite seu desempenho. E ela geralmente vem escrita no próprio aparelho, no adesivo ao na parte de trás ou de baixo do aparelho. 

Vamos usar como exemplo uma lâmpada de LED que tenho na minha luminária, na caixa veio especificando que ela tem potência igual a 7W.

2.    Calcular as horas, por mês, em que o aparelho consome energia:

Como queremos o consumo por mês, então vamos calcular quantos horas nesse período o aparelho permanece consumindo energia. 

No caso da minha lâmpada suponho que por dia ela fique ligada 3h, multiplicando vezes 30 dias (1 mês) é igual a 90h de consumo / mês.

O mesmo você faz no seu cálculo.

3.    Calcular a energia elétrica consumida por mês, pelo aparelho: 

O valor da energia elétrica é dado pela fórmula:

Eel = P(w) . T(h)

P = potência e T = tempo

No caso da lâmpada, já temos o valor de sua potência e do tempo de consumo, médio, por mês. Agora é só fazer a multiplicação: 

Eel = 7. 90 -> Eel = 630w/h

O mesmo é feito para os outros aparelhos.

 

4.    Transforma w/h em kW/h

Como a tarifa de energia é calculada pela unidade de medida kW/h, precisamos transformar w/h, é só dividir por 1000. 

630wh / 1000 ---> 0,63kWh

5.    Calcular o custo, em reais, do consumo de energia do aparelho por mês.

Após realizar todos os cálculos acima, chegamos ao resultado final da energia que é consumida pelo roteador por mês, 0,63kW/h.

Supondo que:

A tarifa de 1 kW/h custa R$0,56374269.
(Essa tarifa você encontra na sua conta de energia)

Assim, para calcular o custo de energia elétrica do roteador, é só fazer uma regra de 3 simples. 

1 kW/h ------ R$0,56374269
0,63kW/h ------ R$0,35

O mesmo você pode fazer para seus aparelhos.

OBS.:

o   Na etiqueta da geladeira não tem a descrição de sua potência, apenas o valor do consumo de energia, por mês, exemplo: 39,8kW/h. Com isso resta apenas multiplicar pela tarifa de energia e chegar ao resultado do valor do consumo.

o   Nos dados da máquina de lavar o consumo de energia é medido por ciclos.

Exemplo:

A cada 1 ciclo se consome 0,24kw/h, de energia.

Supondo que em um mês se realizem 20 ciclos.

O consumo de energia mensal da máquina de lavar é 4,8kW/h ou 4800w/h

Multiplicando 4,8kW/h pela tarifa da conta de energia, o valor corresponde a R$2,70.

o   A unidade de medida da bomba d’agua é HP (sigla inglesa, horse power).

A minha bomba d’água tem potência ½ HP

Transformando HP em Watt:

1 HP ------------ 745,7w
½ HP -------- xw

½ HP = 372,85w

  

Fôrma de Alumínio

Imagine uma casa de 42m² construída em 4 dias, com paredes de concreto, utilizando pouca mão de obra, e gerando quase 0% de resíduo no canteiro. É muito boa a ideia, não é?! Tudo isso é possível, com a utilização das fôrmas de alumínio.

As fôrmas são usadas especialmente para construção de lajes, paredes de concreto, etc. tanto para casa ou prédios e até mesmo obras de infraestrutura. E no canteiro de obra é comum o uso de fôrmas de madeira e para obras de infraestrutura as de aço. Logo a de alumínio torna-se um diferencial no modelo de construção. 

“Forma de madeira é um processo arcaico, muitas vezes não tem padronização e assim a qualidade de execução é menor”  (Roberto Matosinhos, assessor técnico do Sindicato da Indústria da Construção Civil no Estado de Minas Gerais)

As fôrmas de alumínio surgiram nos EUA e chegaram ao Brasil em 1979 e como cada tipo de fôrma possui suas vantagens e desvantagens, essas características é que vão pesar na escolha da construtora. De princípio, falou em repetição de tipologia estrutural e velocidade de construção o uso da fôrma de alumínio é uma ótima escolha. 

A Trisul e a MRV, são exemplos de construtoras que há alguns anos tem investido no uso de fôrmas de alumínio, e a SH é uma empresa líder na venda e locação.  Apesar disso, ainda há pouca divulgação do material e muitas empresas resistem em migrar do processo convencional para as paredes de concreto com fôrmas de alumínio.  O projeto do governo, Minha Casa Minha Vida, deram uma abertura maior ao investimento das fôrmas.  

 “Essas soluções devem crescer porque a construção civil está se industrializando” (Roberto)

A fôrma consiste em painéis de liga de alumínio, formados por perfis entrudados e unidos mecanicamente, o que dispensa o uso de soldas estruturais, a união dos painéis (imagem 1) é feita com pinos e cunhas (imagem 2). Utiliza acessórios, como os alinhadores, aprumadores e plataformas de trabalho. As gravatas (imagem 3) são utilizadas para travar a fôrma. Admitindo pressão de até 60kN/m°. 

Imagem 1 - Painéis

Imagem 2 - Pinos e cunha 

 

Imagem 3  - Gravata

Antes da concretagem, recomenda-se a aplicação desmoldante à base de óleo vegetal e, para auxiliar na limpeza posterior, as peças devem receber jatos de água. No momento de desmolde não se deve martelar as placas. Todos esses cuidados colaboram para a vida útil do material e evita patologias como, fissuras, trincas, falhas na parede. 

Montagem é feita da seguinte forma:

1º Execução do radier ;
2º Marcação no piso das paredes que serão moldadas com as fôrmas de alumínio
3º Instalação dos espaçadores de piso
4º Colocação das telas de aço
5º Instalação das tubulações hidráulicas e elétricas, bem como das caixas de tomadas e interruptores
5º Instalação das fôrmas de parede, com gabaritos para as aberturas (esquadrias)
6º Instalação de fôrmas de laje
7º Concretagem
8º Desforma

https://www.youtube.com/watch?v=gCxoOJkas5c
Eu indico para vocês o vídeo, no link acima, ele é bastante ilustrativo para entender a montagem e desmontagem das fôrmas.

O material possui uma liga especial que diminui seu peso, sem comprometer a resistência, o que permite o transporte manual dispensando o uso de maquinário.  O painel pesa aproximadamente 20kg/m², o manuseio pode ser feito com alças. 

Se comparada a construção com tijolos cerâmicos, economiza-se 40% do tempo.  Outro exemplo que podemos citar, um prédio com 440 apartamentos foi concluído em 12 meses, se fosse com alvenaria o prazo seria de 12 meses.

Manuseado de forma correta e limpo corretamente, o sistema a alcança dois mil ciclos.

O operário não precisa fazer um curso ou se especializar para trabalhar com as fôrmas de alumínio, apenas ser qualificado com um treinamento rápido, simples e efetivo.

Um operador poderá ter várias funções na obra, o carpinteiro poderá trabalhar do início ao fim da obra. 

Dependendo da escala dos empreendimentos da construtora, o custo do imóvel pode cair até 30%. Isso, porque quando reduzimos o tempo de construção refletirá na quantidade de pessoas trabalhando, então será menos custos com funcionários e encargos sociais.  A não locação de equipamentos, e a redução de resíduos também é um fator determinante.  

 A fôrma de alumínio quando não usada em projetos de repetição tipologia estrutural pode se tornar o material mais caro da obra pois, sua aquisição tem um custo elevado.  Porém, quando a construtora investe em um empreendimento de repetição estrutural, como o projeto Minha Casa Minha Vida, condomínios, etc, ao se calcular todos os gastos e comparar ao método tradicional de construção, a fôrma trará vantagens em relação ao custo como já citado anteriormente.

A fôrma de alumínio, é uma “nova” tecnologia ainda no Brasil, e como já foi bem frisado traz muitas vantagens quando usada com objetivo correto. Porém, as construtoras ainda resistem em aderir ao novo modelo um dos motivos é o fornecimento, as empresas têm receio quanto ao tempo estipulado para a entrega da mercadoria e se os fornecedores serão fieis ao projeto, entre outras coisas.

 

 


OBS.: As imagens da fôrma foram retiradas da internet.